Prisma regulată dreaptă

Bun venit! În acest video discutăm despre aria laterală, aria totală şi volumul prismei regulate.

Un poliedru este un corp mărginit de suprafețe plane. Fețele poliedrului sunt poligoane.

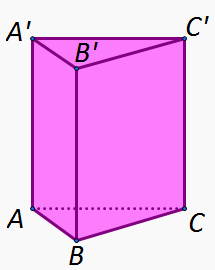
Prisma este un poliedru având două baze- poligoane egale, iar fețele laterale sunt paralelograme și muchiile laterale sunt egale între ele.

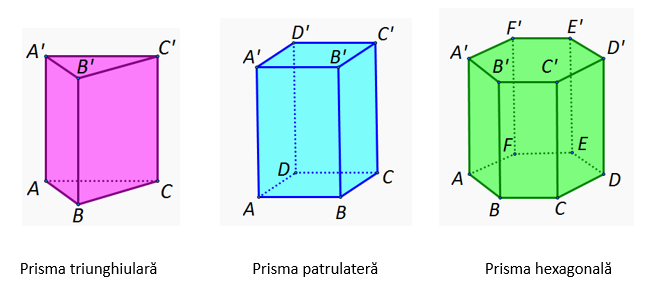
În figura de mai jos, avem un exemplu de prismă având bazele dreptunghiurile ABCD și A’B’C’D’. În funcție de numărul de laturi ale poligonului de la bază, prismele se clasifică în prisme triunghiulare, prisme patrulatere, prisme pentagonale, hexagonale, etc. În figura de mai jos avem o prismă patrulateră.

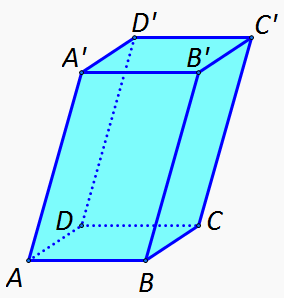
O prismă dreaptă este o prismă cu muchiile laterale perpendiculare pe planul bazei. În acest caz, fețele laterale ale prismei sunt dreptunghiuri.

O prismă regulată este o prismă având bazele poligoane regulate (ex: triunghi echilateral, pătrat, hexagon regulat).

Înălțimea unei prisme este distanța dintre planele bazelor. În cazul prismei drepte, înălțimea este egală cu muchiile laterale.

În continuare vom discuta despre prisme regulate drepte. O să vedem care sunt formulele pentru aria și volumul prismei triunghiulare, aria și volumul prismei patrulatere și a prismei hexagonale.

Aria laterală, aria totală și volumul prismei regulate

A_l = P_b^.h
A_t = A_l + 2A_b
V = A_b^.h

unde: A_l – aria laterală, P_b – perimetrul bazei, h – înălțimea primei, A_t – aria totală, A_b – aria bazei, V – volumul.

Formulele de mai sus sunt valabile pentru orice tip de prismă, iar perimetrul bazei și aria bazei se calculează în funcție de poligonul de la bază.

Prisma triunghiulară regulată are baza triunghi echilateral. Formulele pentru perimetrul bazei și aria bazei sunt:

Prisma patrulateră regulată are baza pătrat. Formulele pentru perimetrul bazei și aria bazei sunt:

Prisma hexagonală regulată are baza hexagon. Formulele pentru perimetrul bazei și aria bazei sunt:

Probleme rezolvate cu prisma regulata dreapta

Problema 1

O prismă triunghiulară regulată dreaptă are latura bazei de 6 cm și diagonala unei fețe laterale de 12 cm. Aflați aria laterală, aria totală și volumul prismei.

Rezolvare:

Vom afla mai întâi înălțimea prismei h=C’C=B’B. Fețele laterale ale unei prisme drepte sunt dreptunghiuri, prin urmare unghiul B’BC este drept și putem aplica teorema lui Pitagora în triunghiul B’BC:

B’B²+BC² = B’C²

B’B²+6² = 12²

B’B² = 144-36 = 108

Baza prismei este triunghi echilateral, iar perimetrul bazei va fi P_b=3l=18 cm. Aria laterală a prismei este perimetrul bazei ori înălțimea și vom obține:

În continuare vom calcula aria bazei (aria triunghiului echilateral):

Aria totală a unei prisme este aria laterală plus ariile celor două baze:

Volumul prismei este produsul dintre aria bazei și înălțime:

Problema 2

O piscină are forma unei prisme patrulatere regulate cu latura bazei de 16 m și înălțimea de 2,5 m. Baza piscinei și pereții laterali se acoperă cu plăci de mozaic. Aflați aria suprafeței ce trebuie acoperită cu mozaic și câți litri de apă intră în piscină, știind că se toarnă apă până la înălțimea de 2 m.

Rezolvare:

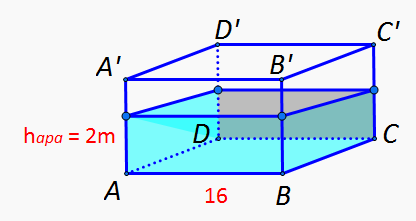
Baza piscinei este un pătrat cu latura de 16 m și vom afla mai întâi perimetrul bazei: P_b=4∙16=64 m.

Să aflăm acum aria laterală a prismei și aria bazei:

Aria suprafeței acoperită cu mozaic este aria laterală împreună cu aria bazei. Atenție! Nu vom aduna două baze, ca și în formula de mai sus, ci doar una, deoarece piscina nu este acoperită.

Volumul apei se calculează înmulțind aria bazei cu înălțimea la care se ridică apa (h=2m):