Sinteză formule Geometrie pentru Evaluarea Națională

Iată principalele formule de geometrie pentru Evaluare Nationala:

Formule de geometrie pentru Evaluare Nationala: Arii și perimetre

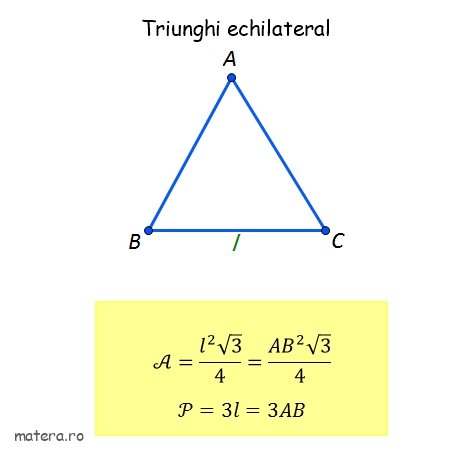
Cercul:

Asemănarea triunghiurilor:

Teoreme în triunghiul dreptunghic:

Funcții trigonometrice:

Poligoane regulate:

Linia mijlocie în triunghi:

MN||BC, \quad MN=\frac{BC}{2} 

Linia mijlocie în trapez:

MN||BC, MN=\frac{AD+BC}{2}

Arii și volume corpuri geometrice:

Cubul și paralelipipedul dreptunghic:

Prisma regulată:

A_l=P_b \cdot h \\[12pt]A_t=A_l+2A_b \\[12pt]V=A_b \cdot h

Perimetrul bazei şi aria bazei se calculează în funcţie de tipul de prismă (adică în funcţie de poligonul de la bază), iar formulele pentru pătrat, triunghi echilateral şi hexagon regulat le găsiţi mai sus.

Piramida regulată:

Pentru orice piramidă regulată au loc formulele:

A_l=\frac{P_b\cdot a_p}{2} \\A_t=A_l+A_b\\V=\frac{A_b\cdot h}{3} 

Perimetrul bazei şi aria bazei se calculează în funcţie de tipul de piramidă (adică în funcţie de poligonul de la bază), iar formulele pentru pătrat, triunghi echilateral şi hexagon regulat le găsiţi mai sus.

Tetraedrul regulat

In particular, formulele pentru tetraedru regulat (piramida triunghiulară cu toate muchiile congruente, deci toate fețele triunghiuri echilaterale) sunt:

A_l=3 \cdot A_{tr.echil}=\frac{3l^2\sqrt3}{4}\\[12pt] A_t=4 \cdot A_{tr.echil}=l^2 \sqrt3\\[12pt] V=\frac{1}{3}\cdot \frac{l^2 \sqrt3}{4}\cdot h \space \space sau \space \space V=\frac{l^3\sqrt2}{12}, \\ deoarece \space h=\frac{l\sqrt6}{3}

Trunchiul de piramidă regulată

Pentru orice trunchi de piramidă regulată (patrulateră, triunghiulară, hexagonală) au loc formulele:

A_l=\frac{(P_B+P_b)\cdot a_t}{2} \\A_t=A_l+A_B+A_b\\ V=\frac{h}{3}(A_B+A_b+\sqrt{A_B \cdot A_b})

Cilindrul circular drept

A_l=2\pi RG \\ A_t=2\pi R(R+G)\\ V=\pi R^2h

Conul circular drept

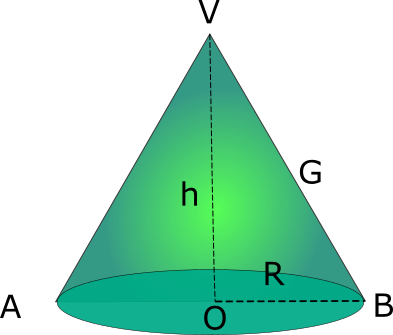
A_l=\pi RG\\A_t=\pi R(R+G)\\ V=\frac{\pi R^2h}{3}\\ 

Dacă notăm cu u măsura unghiului la centru corespunzător sectorului de cerc ce reprezintă aria laterală a conului, atunci:

u \degree=\frac{360 \degree \cdot R}{G}

Trunchi de con circular drept

A_l=\pi G (R+r) \\ A_t= \pi G(R+r)+\pi R^2+\pi r^2 \\ V=\frac{\pi h}{3}(R^2+r^2+Rr)

Sfera

A=4\pi R^2\\ V=\frac{4\pi R^3}{3}.

Citește și articoulul Sinteză formule algebră pentru Evaluarea Natională.