Triunghiul dreptunghic

Bun venit! În această lecţie discutăm despre proprietăţi şi teoreme în triunghiul dreptunghic.

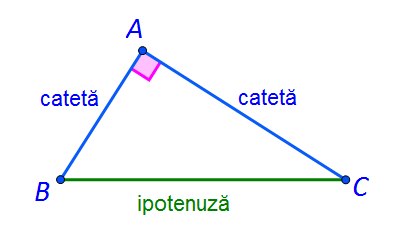
Triunghiul dreptunghic este triunghiul care are un unghi drept (cu măsura de 90°).

Laturile care formează unghiul drept se numesc catete, iar latura opusă unghiului drept se numește ipotenuză.

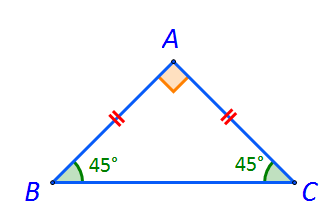
Un triunghi dreptunghic care are catetele congruente se numește triunghi dreptunghic isoscel. În acest caz, unghiurile ascuțite sunt congruente și au măsura egală cu 45° (pentru că (180°-90°):2=45°).

Proprietățile triunghiului dreptunghic

Proprietatea 1. Într-un triunghi dreptunghic, unghiurile ascuțite sunt complementare.

∡B+∡C=90°.

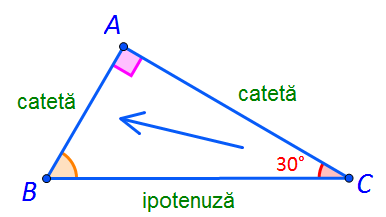
Proprietatea 2. Dacă un triunghi dreptunghic are un unghi cu măsura de 30 de grade, atunci cateta opusă acestui unghi este jumătate din ipotenuză.

AB = BC/2.

Proprietatea 3. Într-un triunghi dreptunghic, mediana corespunzătoare ipotenuzei este jumătate din ipotenuză.

AM- mediană (M mijlocul lui BC) ⟹ AM = BC/2.

Teorema lui Pitagora. În orice triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei.

AB²+AC² = BC²
a² = b² + c²

Pentru elevii din clasa a VII-a, menționăm și formulele de calcul pentru aria unui triunghi dreptunghic:

Aria triunghiului dreptunghic

Aria unui triunghi dreptunghic se poate scrie în două moduri:

• Dacă notăm cele două catete cu c₁ și c₂, atunci formula pentru arie este semiprodusul catetelor:

• Dacă notăm cu i– ipotenuza triunghiului și cu h– înălțimea corespunzătoare ei, atunci aria triunghiului se calculează folosind formula:

Probleme rezolvate – Teoreme în triunghiul dreptunghic

Problema 1

Fie ABC un triunghi dreptunghic în A, cu ∡B=30°. Dacă BC=18 cm, aflați lungimea laturii AC.

Rezolvare:

Latura AC este catetă opusă unghiului de 30°, prin urmare ea va fi jumătate din ipotenuză.

AC = BC/2 = 18:2 =9 cm.

Problema 2

În figura de mai jos, triunghiul MNP este dreptunghic în M, iar O este mijlocul lui NP. Știind că PO=4 cm, aflați lungimea segmentului MO.

Rezolvare:

Dacă O este mijlocul lui NP, atunci PO = ON = 4 cm. Prin urmare, PN = 4+4 = 8 cm.

MO este mediană și ea va fi jumătate din ipotenuză: MO = PN/2 = 8:2 = 4 cm.

Problema 3

Fie ABC un triunghi isoscel cu ∡A=120° și fie M mijlocul laturii BC. Dacă AB=6 cm, aflați lungimea segmentului AM.

Rezolvare:

Dacă triunghiul ABC este isoscel, atunci ∡B=∡C=(180° -120°):2=30°.

AM este mediană în triunghiul isoscel ABC, prin urmare ea va fi și bisectoare și înălțime.

∡BAM = ∡CAM = ∡BAC:2 = 120°:2 = 60°.

Triunghiul AMB este dreptunghic în M, iar AM este cateta opusă unghiului de 30 de grade, așadar AM = AB/2 = 6/2 = 3 cm.