Cercul

Bun venit! În această lecţie discutăm despre o noţiune foarte importantă: cercul şi despre rază, diametru, unghi la centru. Citeşte noţiunile prezentate mai jos, apoi urmăreşte lecţia video pentru a înţelege mai bine.

Cercul este mulțimea punctelor din plan egal depărtate de un punct fix, numit centru, notat de obicei cu O.

Raza unui cerc este segmentul care unește centrul cercului cu un punct de pe cerc. În figura de mai jos, OA este rază.

Un segment care unește două puncte de pe cerc se numește coardă. În figura 2, segmentul AB este o coardă.

O coardă care trece prin centrul cercului se numește diametru. Într-un cerc, diametrul este cea mai lungă dintre coarde. Extremitățile diametrului se numesc puncte diametral opuse. Lungimea unui diametru este egală cu dublul razei:

d = 2r.

Punctele A și B determină pe un cerc două arce: un arc mic, adică porțiunea de cerc aflată în interiorul unghiului AOB și un arc mare, adică porțiunea de cerc din exteriorul unghiului AOB. Arcele se măsoară în grade. Un cerc are 360 de grade. Dacă extremitățile unui arc de cerc sunt puncte diametral opuse, atunci arcul se numește semicerc. Un semicerc are 180 de grade.

Unghi la centru

Un unghi al cărui vârf este centrul cercului se numește unghi la centru. În figura 2, unghiul AOB este unghi la centru.

Măsura unui unghi la centru este egală cu măsura arcului de cerc corespunzător.

Pozițiile unei drepte față de un cerc

• O dreaptă care nu are niciun punct comun cu cercul se numește exterioară cercului.
• O dreaptă care intersectează cercul în două puncte se numește secantă cercului.
• O dreaptă care are un singur punct comun cu cercul se numește tangentă. Tangenta este întotdeauna perpendiculară pe rază în punctul de contact cu cercul.

Urmăriți lecția video de mai jos pentru a înțelege mai bine aceste noțiuni. Lecția se continuă mai jos cu probleme rezolvate.

Probleme rezolvate cu cerc

1. Aflați diametrul unui cerc cu raza r=3 cm.

Rezolvare:

d=2r=2^.3=6 cm.

2. Aflați raza unui cerc având diametrul de 11 cm.

Rezolvare:

d=2r
r=d:2
r=11:2
r=5,5 cm.

3. În figura de mai jos, măsura unghiului AOB este de 73^o. Aflați măsura arcului mic AB și măsura arcului mare AMB.

Rezolvare:

Măsura unghiului la centru este egală cu măsura arcului de cerc cuprins între laturile sale.

4. În figura de mai jos, unghiul AOB are măsura de 60 de grade și dreapta a este tangentă la cerc în punctul B. Ducem prin punctul O dreapta b paralelă cu dreapta a, care intersectează cercul în punctul C. Aflați măsura unghiului AOC.

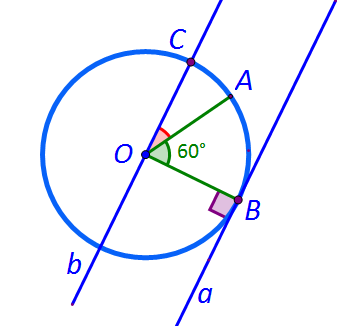
Rezolvare:

Tangenta la cerc este perpendiculară pe rază. Dacă dreptele a și b sunt paralele și considerăm secanta OB, atunci se formează o pereche de unghiuri alterne interne congruente, având măsura de 90 de grade. Așadar, unghiul COB are măsura de 90 de grade.