Conul și trunchiul de con circular drept
Bine ai venit! În această lecţie discutăm despre conul şi trunchiul de con circular drept şi o să vedem care sunt fomulele pentru aria şi volumul conului, aria şi volumul trunchiului de con.
1.Conul circular drept
O dreaptă numită generatoare, care trece printr-un punct fix V și se sprijină pe un cerc descrie o suprafață conică circulară. Conul circular este un corp mărginit de o suprafață conică circulară și de un plan care nu trece prin punctul V. Suprafața conică determină pe acest plan baza conului, iar punctul V se numește vârful conului. Dacă perpendiculara din V pe planul bazei trece prin centrul acesteia, atunci conul circular este drept.

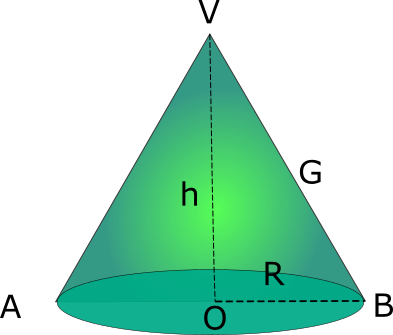
Elementele conului circular drept
- Baza conului: cercul de centru O și rază R;
- Generatoarea: G = VA = VB;
- Înălțimea conului: distanța de la V la planul bazei: h = VO;
Având în vedere că triunghiul VOB este dreptunghic, are loc următoarea relație între rază, înălțime și generatoare:
h2 + R2 = G2
Secționând conul cu un plan care conține dreapta VO se obține secțiunea axială a conului. Prin urmare, secțiunea axială a conului este triunghiul isoscel VAB.
Suprafața laterală a conului se desfășoară în plan după un sector circular a cărui rază este VA, adică generatoarea conului.

Aria laterală, aria totală și volumul conului circular drept
Al = πRG
At = Al + Ab = πRG + πR2 = πR(G+R)
V = πR2h/3
Dacă notăm cu u măsura unghiului la centru corespunzător sectorului de cerc și egalând aria sectorului cu aria laterală a conului, obținem următoarea relație:
u° = 360°∙R/G
Probleme rezolvate cu conul circular drept
Problema 1
Un con circular drept are perimetrul secțiunii axiale de 36 cm, iar raza cercului de la bază este de 5 cm. Aflați:
a) Aria latelară, aria totală a conului.
b) Volumul conului.
Rezolvare:

a) Secțiunea axială este triunghiul isoscel VAB având perimetrul P = 36 cm.
Știm că R = OB = 5 cm, prin urmare AB = AO + OB = 5 + 5 = 10 cm.
P = VA + VB + AB = 2VB + AB = 2G + 10 = 36 cm
2G + 10 = 36
2G = 36 – 10 = 26
G = 26:2 = 13 cm.
Al = πRG = π∙5∙13 = 65π cm2
At = πR(G+R) = π∙5∙(13+5) = 90π cm2
b) Pentru a calcula volumul conului, trebuie mai întâi să aflăm înălțimea h. Pentru aceasta vom aplica teorema lui Pitagora în triunghiul dreptunghic VOB:
VO2 + OB2 = VB2
h2 + R2 = G2
h2 + 52 = 132
h2 = 169 – 25 = 144 și obținem că h = 12 cm.
V = πR2h/3 = π∙25∙12/3 = 100π cm3.
2. Trunchiul de con circular drept
Trunchiul de con circular drept este corpul obținut prin secționarea unui con circular drept cu un plan paralel cu baza și îndepărtarea conului de sus.

Elementele trunchiului de con circular drept
- Baza mare: cercul de centru O și rază R;
- Baza mică: cercul de centru O’ și rază r;
- Generatoarea: G = AA’ = BB’;
- Înălțimea: distanța dintre cele două baze: h = O’O.
Secțiunea axială a trunchiului de con circular drept este trapezul isoscel ABB’A’.
Aria laterală, aria totală și volumul trunchiului de con circular drept
Al = πG(R + r)
At = Al + AB + Ab = πG(R + r) + πR2 +πr2
V = πh(R2 + r2 + Rr)/3.




Un comentariu
Cristi
Fa te rog un video ca sa il inteleg mai bine